Let us embark on an insightful exploration into causal effects within machine learning and data science. In this blog, we will delve into causal estimation methods, emphasizing their importance in addressing complex business problems and decision-making processes.This comprehensive guide aims to shed light on crucial methodologies that unlock deeper insights in Causal AI. This blog is in continuation to our earlier blogs on causal analysis dealing with the following topics

1. Estimating the effect on loyalty program
2. Back door, front door and instrument analysis in causal AI
3. Causal graphs
4. Confounders , Treatment and Control groups

We will take the discussions forward dealing with different methods to estimate the causal effect in this blog. Let us look at the contents of this article.

Structure

1. Business context ( Introduction to potential outcomes, individual treatment effect and average treatment effect
2. Causal estimation from scratch using Linear regression
   • Synthetic data generation for the problem statement
   • Fitting a linear model to map the causal relationship
   • Intervention and Average Treatment Effect Estimation
   • Quantifying Impact: Calculating ATE through difference in expected outcomes
   • Interpretation of results
3. Causal estimation using Dowhy library
4. Applications of causal estimation techniques in different domains
   • Marketing
   • Finance
   • Healthcare
   • Retail
5. Conclusion

1.0 Business Context

We will start our discussions with a practical problem. Imagine a tailored tutoring program for students, designed to assess its influence on each student’s academic performance.This real-world business problem sets the stage for understanding the concepts of treatment and outcomes which we have learned earlier in the previous article. Here, the tutoring program acts as the treatment, and the resulting change in academic performance becomes the outcome.

When discussing causal estimation its important to explore the concept of potential outcomes (PE). Potential outcomes refer to the different results a student could achieve under two conditions: one with the tutoring program (treatment) and the other without it (no treatment). In the context of our business problem, each student has the potential to demonstrate varied academic performances depending on whether they undergo the tutoring program or not. This introduces the concept of Individual Treatment Effect (ITE), representing the specific causal impact of the treatment for an individual student. However, a significant challenge arises as we can only observe one outcome per student, making it impossible to directly measure both potential outcomes. For instance, if a student improves their academic performance after participating in the tutoring program, we can witness this positive outcome. However, we cannot simultaneously observe the outcome that would have occurred if the same student did not receive the tutoring.

This challenge necessitates the need for the concept of Average Treatment Effect (ATE), providing a broader perspective by considering the average impact across the entire group of students. In the previous paragraph we saw the challenge with ITE. The way around this challenge is by ATE. Here, the ATE steps in, offering a comprehensive understanding of the overall effectiveness of the tutoring program across the entire student population. ATE allows us to aggregate these individual treatment effects, providing a holistic view of how the program influences academic performance across the diverse student population.

As we navigate the intricacies of causal estimation methods, the interplay between ITE and ATE emerges as a key focal point. This exploration not only addresses the complexities of our business problem but also sets the stage for robust analyses into treatment effects within various contexts. Throughout this comprehensive guide, we’ll uncover various methods, including causal estimation using linear regression, propensity score matching, and instrumental variable analysis, to estimate the potential outcomes of treatments.

In this article we will dive deep into the estimation method using linear regression. We will be dealing with other methods in subsequent articles.

2.0 Causal estimation from scratch using Linear regression

Regression analysis is a data analysis method that aims to comprehend the connections between variables and unveil cause-and-effect patterns. For example, when investigating the impact of a new study technique on exam scores, regression analysis allows us to account for factors such as study time, sleep, and past grades. This systematic approach facilitates a quantitative assessment of the study technique’s impact while considering the influence of these additional variables.

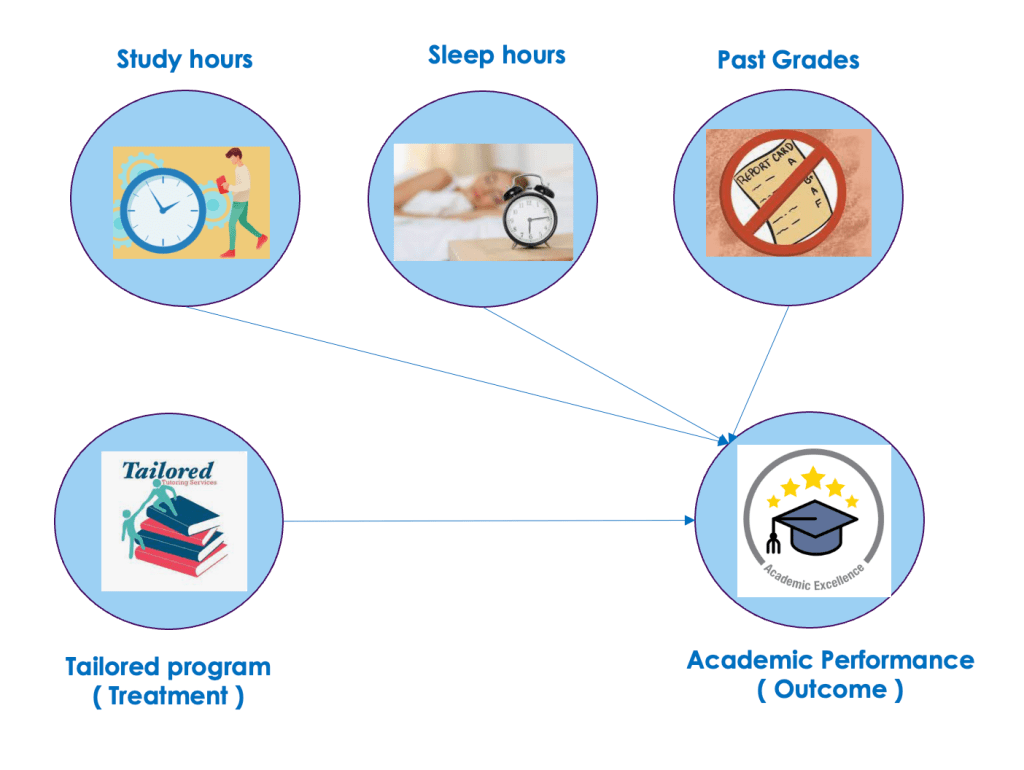
In practical terms, you can employ regression analysis to explore how hours spent exercising affect weight loss, factoring in elements like diet and metabolism. This method proves valuable for complex questions with multiple variables. However, it is most effective when certain assumptions hold true, making it suitable for straightforward relationships without hidden factors affecting both the treatment and the outcome.

Let us start by generating synthetic data for our exercise with 100 students. The students have random study hours, sleep hours, and past grades.

2.1 Synthetic data generation for the analysis

import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression

n_students = 100
study_hours = np.random.randint(1, 10, n_students)
sleep_hours = np.random.randint(5, 9, n_students)
past_grades = np.random.randint(60, 100, n_students)

Next a dataFrame is created with columns for study hours, sleep hours, past grades, and a binary column representing whether or not a student received the new study technique (0 for No, 1 for Yes).

data = pd.DataFrame({
    'StudyHours': study_hours,
    'SleepHours': sleep_hours,
    'PastGrades': past_grades,
    'NewStudyTechnique': np.random.choice([0, 1], n_students)
})

Next we generate a ‘DoExamScores’ column using a formula incorporating study hours, sleep hours, past grades, and the influence of the innovative study technique. To emulate real-world variations, we introduce random noise into the equation. This new variable serves as a key indicator, amalgamating crucial factors that contribute to exam performance.

data['DoExamScores'] = (
    70 + 2 * data['StudyHours'] + 3 * data['SleepHours'] + 5 * data['PastGrades'] +
    10 * data['NewStudyTechnique'] + np.random.normal(0, 5, n_students)
)

2.2 Fitting a linear model to map the causal relationship

We will now perform causal analysis using regression analysis on the data. The data will be split into features (X_do) and the target variable (y_do). A linear regression model is then fitted to estimate the relationship between the features and the target variable.

X_do = data[['StudyHours', 'SleepHours', 'PastGrades', 'NewStudyTechnique']]
y_do = data['DoExamScores']

model = LinearRegression()
model.fit(X_do, y_do)

2.3 Intervention and Average Treatment Effect Estimation

In the pursuit of estimating the Average Treatment Effect (ATE), we employ the concept of intervention, a pivotal step in causal analysis. Intervention, represented by the “do” operator, allows us to explore hypothetical scenarios by directly manipulating the treatment variable. This step is crucial for uncovering the causal impact of a specific treatment, irrespective of the actual treatment status of individuals.

Different from conditioning, where we analyze outcomes within specific groups based on the actual treatment received, intervention delves into the counterfactual—what would happen if everyone were exposed to the treatment, and conversely, if no one were. It provides a deeper understanding of the causal relationship, untangling the impact of the treatment from the complexities of observed data. Let us observe the code on how we achieve that

# Getting the intervention data sets
X_do_1 = pd.DataFrame.copy(X_do)
X_do_1['NewStudyTechnique'] = 1
X_do_0 = pd.DataFrame.copy(X_do)
X_do_0['NewStudyTechnique'] = 0

In our provided code, the concept of intervention comes to life with the creation of two datasets, X_do_1 and X_do_0, representing scenarios where everyone either received or did not receive the new study technique. By simulating these intervention scenarios and observing the resultant changes in predicted exam scores, we can effectively estimate the Average Treatment Effect, a critical measure in causal analysis. This process allows us to grasp the counterfactual world, answering the essential question of how the treatment influences the outcome when universally applied.

2.4 Quantifying Impact: Calculating ATE through difference in expected outcomes

Now that we have dealt with the counterfactual question, let us look at the answer we were looking at. Whether the new study technique was indeed effective. This can be unravelled by calculating the average treatment effect, which can get as follows.

ate_est = np.mean(model.predict(X_do_1) - model.predict(X_do_0))

The code for Average Treatment Effect (ATE) estimation, represented by ate_est = np.mean(model.predict(X_do_1) - model.predict(X_do_0)), calculates the mean difference in predicted outcomes between the scenarios where the new study technique is applied (X_do_1) and where it is not applied (X_do_0).

2.5 Interpretation of the results

• The model.predict(X_do_1) represents the predicted outcomes when all individuals are exposed to the new study technique.
• The model.predict(X_do_0) represents the predicted outcomes in a hypothetical scenario where none of the individuals are exposed to the new study technique.

The subtraction of these predicted outcomes gives the difference in outcomes between the two scenarios for each individual. Taking the mean of these differences provides the ATE, which represents the average impact of the new study technique across the entire group.

In this specific example:

• The calculated ATE value of 9.53 suggests that, on average, the new study technique is associated with a positive change in the predicted outcomes.
• This positive ATE indicates that, overall, the new study technique has a favorable impact on the exam scores of the students.

This interpretation aligns with the initial question of whether the new study technique is effective. The positive ATE value supports the hypothesis that the implementation of the new study technique contributes positively to the predicted exam scores, providing evidence of its effectiveness based on the model’s predictions.

Alternatively in a linear regression model, the coefficient of the treatment variable (‘NewStudyTechnique’) represents the change in the outcome variable for a one-unit change in the treatment variable. In this context, it gives us the estimated causal effect of the new study technique on exam scores, making it equivalent to the ATE.

ate_est = model.coef_[3]
print('ATE estimate:', ate_est)

We can see that both these values match.

3.0 Implementation of the example using DoWhy library

In our earlier implementation, we manually crafted a linear regression model and calculated the Average Treatment Effect (ATE) by manipulating treatment variables. The idea of the earlier implementation was to get an intuitive idea of what is happening behind the hood. Alternatively we now leverage the DoWhy library, a powerful tool designed for causal inference and analysis. DoWhy simplifies the process of creating causal models and estimating treatment effects by providing a unified interface for causal analysis.

import pandas as pd
import numpy as np
import dowhy
from dowhy import CausalModel

# Generate the data
n_students = 100
study_hours = np.random.randint(1, 10, n_students)
sleep_hours = np.random.randint(5, 9, n_students)
past_grades = np.random.randint(60, 100, n_students)

data = pd.DataFrame({
    'StudyHours': study_hours,
    'SleepHours': sleep_hours,
    'PastGrades': past_grades,
    'NewStudyTechnique': np.random.choice([0, 1], n_students)
})

data['DoExamScores'] = (
    70 + 2 * data['StudyHours'] + 3 * data['SleepHours'] + 5 * data['PastGrades'] +
    10 * data['NewStudyTechnique'] + np.random.normal(0, 5, n_students)
)

# Define the causal model
model = CausalModel(
    data=data,
    treatment='NewStudyTechnique',
    outcome='DoExamScores',
    common_causes=['StudyHours', 'SleepHours', 'PastGrades']
)

# Identify the causal effect using linear regression
identified_estimand = model.identify_effect(proceed_when_unidentifiable=True)
estimate = model.estimate_effect(identified_estimand, method_name="backdoor.linear_regression")

# Print the causal effect estimate
print(estimate.value)

In the implementation the creation of data set is the same as we have seen earlier. After creating the data frame we define a causal model using the CausalModel class from DoWhy. We specify the treatment variable (‘NewStudyTechnique’), the outcome variable (‘DoExamScores’), and the potential common causes or confounders (‘StudyHours’, ‘SleepHours’, ‘PastGrades’).

The identify_effect method is called to identify the causal effect based on the specified causal model. This step involves determining the causal estimand, considering potential backdoor and front-door paths in the causal graph. To know more about back door and front door paths you can refer our previous blogs.

With the identified estimand, we proceed to estimate the causal effect using linear regression as the chosen method. The backdoor.linear_regression method is employed to handle the backdoor paths and calculate the effect of the treatment variable on the outcome. We can see from the output, that both methods give very similar results.

The DoWhy implementation provides a more automated and standardized approach to causal analysis by handling various aspects of the causal graph, identification, and estimation, streamlining the process compared to the manual implementation from scratch.

4.0 Applications of causal estimation techniques in different domains

Causal estimation is crucial for moving beyond correlation and understanding the true cause-and-effect relationships that drive outcomes. Linear regression, as a versatile tool, empowers professionals in marketing, finance, healthcare, retail, to name a few, to make data-driven decisions, optimize strategies, and improve overall performance. The significance of causal estimation lies in its ability to guide interventions, enhance predictive modeling, and provide a deeper understanding of the factors influencing complex systems. Let us look at potential use cases in different domains

4.1 Marketing:

Causal estimation using linear regression is instrumental in the field of marketing, where businesses aim to comprehend the effectiveness of their advertising strategies. In this context, the treatment could be the implementation of a specific advertising campaign, the outcome might be changes in consumer behavior or purchasing patterns, and potential confounders could include factors like seasonality, economic conditions, or competitor actions. By employing linear regression, marketers can isolate the impact of their advertising efforts, discerning which strategies contribute most significantly to desired outcomes. This approach enhances marketing ROI and aids in strategic decision-making.

4.2 Finance:

In finance, causal estimation with linear regression can be applied to unravel the complex relationships between economic factors and investment returns. Here, the treatment might represent changes in interest rates or economic policies, the outcome could be fluctuations in stock prices, and potential confounders may encompass market trends, geopolitical events, or industry-specific factors. By employing linear regression, financial analysts can discern the true impact of economic variables on investment performance, facilitating more informed portfolio management and risk assessment.

4.3 Healthcare:

Causal estimation using linear regression is paramount in healthcare for evaluating the effectiveness of different treatments and interventions. The treatment variable might represent a specific medical intervention, the outcome could be patient health outcomes or recovery rates, and potential confounders may include patient demographics, pre-existing health conditions, and lifestyle factors. Linear regression allows healthcare professionals to disentangle the impact of various treatments from confounding variables, aiding in evidence-based medical decision-making and personalized patient care.

4.4 Retail:

In the retail sector, understanding customer behavior is essential, and causal estimation with linear regression provides valuable insights. The treatment in this context might be changes in pricing strategies or promotional activities, the outcome could be changes in customer purchasing behavior, and potential confounders may involve external factors like economic conditions or competitor actions. By employing linear regression, retailers can identify the causal factors influencing customer decisions, allowing for more targeted and effective retail strategies.

5.0 Conclusion

The exploration of causal estimation methods unravels a powerful toolkit for understanding and deciphering complex cause-and-effect relationships in various domains. Whether applied to optimize marketing strategies, inform financial decisions, enhance healthcare interventions, or refine retail operations, causal estimation methods provide a nuanced lens through which to interpret data and guide decision-making. From the foundational concepts of potential outcomes to the intricacies of linear regression and sophisticated frameworks like DoWhy, this journey through causal estimation has underscored the importance of moving beyond mere correlation to discern true causal links.

As we embrace the significance of causal estimation in our data-driven era, the ongoing quest for refined methodologies and deeper insights continues. Whether in marketing, finance, healthcare, retail, or beyond, the application of causal estimation methods stands as a testament to the ever-evolving nature of data science and its profound impact on shaping a more informed and effective future.